Modelling ¶
Nature is often more complicated than it seems. In order to study it, scientists often develop models that represent reality in a simplified manner. Working with models has become a significant part of our research at the WSL.
Contents ¶
Thanks to the ever-increasing power of computers, modelling has been gaining enormously in importance over the last few years. However, models per se are nothing new: the first scientific model probably had its origins with the Greek philosopher Aristotle, who developed a model of the solar system that was supposed to explain the collected observations of the sky and predict planetary positions.
Although models are often substantial simplifications of reality, they have become indispensable to science, with applications ranging from meteorology (weather forecasting) to healthcare (e.g. spread of epidemics) to chemistry (e.g. air pollution) to environmental science. At the WSL, we develop and use models to simulate the habitats of plants and animals, for example, or to predict rockfalls.
Many results and easy on the environment ¶
Models allow us to generate many results in a short time and to run different scenarios by varying the baseline conditions. Moreover, researchers can use models to carry out experiments that cause no harm to the environment, for example in rockfall simulations (LINK to RAMMS:Rockfall). Models can also reveal possible relationships in nature which would not be apparent by mere observation.
One thing that models have in common is that they are expressed with mathematical equations or rules. The equations are usually too difficult to solve in one's head or on paper, so the computer takes this work on. Scientific models are often so complicated that the exact solution cannot even be calculated by a computer; the equations cannot be solved analytically. Therefore, the solution is approximated by numerical methods; these are referred to as numerical models.
Packaging nature in equations ¶
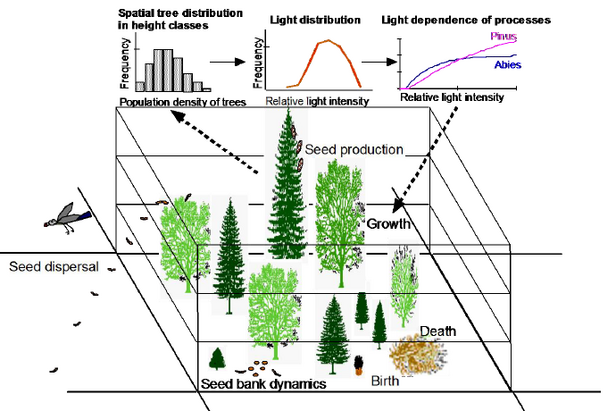
Translating environmental processes into the language of mathematics plays a central role in the modelling of ecosystems or natural hazards, because processes in nature are interwoven; tree growth is influenced by temperature, precipitation, nutrients and neighbouring trees. The challenge is to package these processes into concrete formulas and, above all, to quantify the symbols in the formulas.
Depending on the approach, we can divide models into several categories:
Physical models
A physical model is based on a mathematical equation which, in turn, is based on a physical process such as diffusion, melting processes or heat transfer. For example, at the WSL, we model hydrological processes in snow in order to better assess the risk of flooding.
Statistical models
Statistical models are based on observations. They correlate at least two data series, such as temperature and different tree species. This gives a distribution of the tree species at different temperatures. With this, researchers can feed simulations which investigate the propagation of different tree species under climate change conditions.
Dynamic models
Dynamic models describe how a value, such as the number of trees, changes in a forest. This change is dependent on various factors which, in turn, can exert a reciprocal influence on each other: the health of the trees, of neighbouring trees or environmental conditions.
Theoretical models
Relatively simple mathematical equations describe the dynamics of biotic communities. For example, the classic Lotka-Volterra predator-prey equations formulate the relationship between predators and prey. Competitive or symbiotic relationships are formulated in theoretical models. They describe how species impede each other or benefit from each other.
Agent-based models
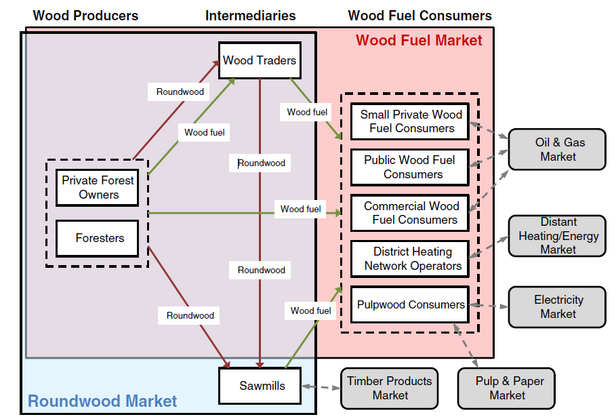
Another approach is agent-based models, which, however, have nothing to do with 007. Agents are decision-makers whose behaviour influences the development of a system. This means that the development is not prescribed by the system – for example, as in physical models by physical processes – but results from how the agents behave. At WSL, for example, we are investigating in a project how the wood fuel market reacts to decisions made by different "agents": Foresters, timber traders, forest owners or sawmills.