Theoretical community stability
2016 - 2025
With theoretical analysis and simulations of Lotka-Volterra competition models, we study the stability of communities, in terms of a) multiple equilibria, b) competition strengths and c) effects of - potentially environment driven - changes in demographic parameters.
Lotka-Volterra competition model ¶
\( \frac{dx_i}{dt}= x_i r_i (1- \frac{ \sum\limits_{j=1}^{n} {x_j \alpha_{ij}}}{K_i}), i=1...n, x_i, r_i,K_i,\alpha_{ij} >=0\)
The xi is the abundance (such as population density, biomass, LAI, basal area,...) of the species i in a given species pool, ri its intrinsic growth rate, Ki its carrying capacity, and \(\alpha_{ij}\) the strength of species j's competition to species i, relative to the intraspecific competition of species i to itself.
This model can have many equilibria with non-negative, i.e., ecologically meaningful abundances. Of these either one (global stability) or multiple (multistability) can be stable. Each stable equilibrium corresponds to a community. If there are multiple stable equilibria, a perturbation in the abundances can lead to a switch between the equilibria. Also changes in the parameters can lead to the loss or gain of stability in globally stable or multiple equilibria.
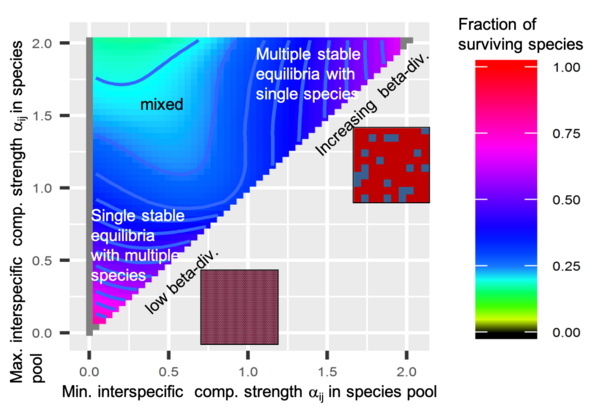
Multiple equilibria ¶
We developed a new method (COMMUSTIX) which is able to detect all positive stable equilibria of a given species pool (Lischke & Löffler, 2017). The method combines theoretical filters based on non-negativity of equilibria and the eigenvalues of the Jacobian matrix with an efficient algorithm which tests whether the Jacobian eigenvalues of the remaining species combinations are all negative (a condition for stability).
Exploring numerous large species pools with this method revealed that the number of multiple equilibria depends strongly on the range of competition strengths within the species pool: for pools with weak interactions global equilibria with many species were found, for pools with strong competition many equilibria with few down to single species were found. For species pools with very different interactions, global and multiple equilibria could happen (Lischke & Löffler, 2017).